Talks
 February, 2025
February, 2025

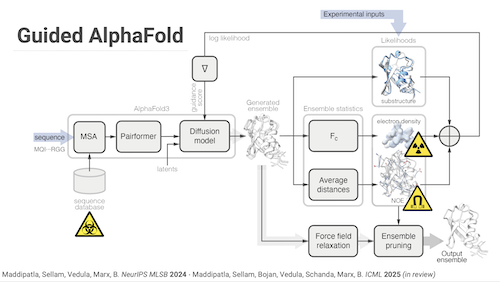
Proteins exist as a dynamic ensemble of multiple conformations, and these motions are often crucial for their functions. However, current structure prediction methods predominantly yield a single conformation, overlooking the conformational heterogeneity revealed by diverse experimental modalities. Here, we present a framework for building experiment-grounded protein structure generative models that infer conformational ensembles consistent with measured experimental data. The key idea is to treat state-of-the-art protein structure predictors (e.g., AlphaFold3) as sequence-conditioned structural priors, and cast ensemble modeling as posterior inference of protein structures given experimental measurements. Through extensive real-data experiments, we demonstrate our method’s generality to incorporate various experimental measurements. In particular, our framework uncovers previously unmodeled conformational heterogeneity from crystallographic densities, generates high-accuracy NMR ensembles orders of magnitude faster than the status quo, and incorporates pair-wise cross-link constraints. Notably, we demonstrate that our ensembles outperform AlphaFold3 and sometimes better fit experimental data than publicly deposited structures to the Protein Data Bank (PDB). We believe that this approach will unlock building predictive models that fully embrace experimentally observed conformational diversity.
 May, 2023
May, 2023

The fact that some amino acid chains fold alone into natively structured and fully functional proteins in solution, has led to the commonly accepted “one sequence-one structure” notion. However, within the cell, protein chains are not formed in isolation, to fold alone once produced. Rather, they are translated from genetic coding instructions (for which many versions exist to code a single amino acid sequence) and begin to fold before the chain has fully formed through a process known as co-translational folding. The effect of coding and co-translational folding mechanisms on the final protein structure are not well understood and there are no studies showing side by side structural analysis of protein pairs having alternative synonymous coding. We are using the wealth of high resolution protein structures available in the Protein Data Bank to computationally explore the association between genetic coding and local protein structure and pinpoint positions of alternate conformations in homologous proteins which cannot be readily explained by the amino acid sequence or protein environment.
 November, 2021
November, 2021

In this talk, I will show how recent advances in computational imaging and machine learning allow building radically new camera designs teaching the machines to see.
 December 17, 2019
December 17, 2019

We address the problem of reconstructing a matrix from a subset of its entries. Current methods, branded as geometric matrix completion, augment classical rank regularization techniques by incorporating geometric information into the solution. This information is usually provided as graphs encoding relations between rows/columns. In this work, we propose a simple spectral approach for solving the matrix completion problem, via the framework of functional maps. We introduce the zoomout loss, a multiresolution spectral geometric loss inspired by recent advances in shape correspondence, whose minimization leads to state-of-the-art results on various recommender systems datasets. Surprisingly, for some datasets, we were able to achieve comparable results even without incorporating geometric information. This puts into question both the quality of such information and current methods’ ability to use it in a meaningful and efficient way.
 April 17, 2019
April 17, 2019

In this talk, I show several learning-based approaches to tackle deformable shape correspondence problems. I also present a completely unsupervised way of learning correspondence overcoming the need for the expensive annotated data. I showcase these methods on a wide selection of correspondence benchmarks, where they outperform other techniques in terms of accuracy, generalization error, and efficiency.
 September 26, 2018
September 26, 2018

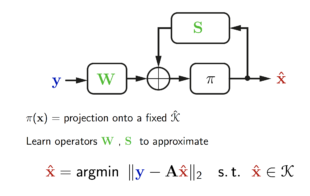
Solving a linear system of the type Ax + n = y with many more unknowns than equations is a fundamental ingredient in a plethora of applications. The classical approach to this inverse problem is by formulating an optimization problem consisting a data fidelity term and a signal prior, and minimizing it using an iterative algorithm. Imagine we have a wonderful iterative algorithm but real-time limitations allows only to execute five iterations thereof. Will it achieve the best accuracy within this budget? Imagine another setting in which an iterative algorithm pursues a certain data model, which is known to be accurate only to a certain amount. Can this knowledge be used to design faster iterations? In this talk, I will try to answer these questions by showing how the introduction of smartly controlled inaccuracy can significantly increase the convergence speed of iterative algorithms used to solve various inverse problems. I will also elucidate connections to deep learning an provide a theoretical justification of the very successful LISTA networks. Examples of applications in computational imaging and audio processing will be provided.
 January 29, 2018
January 29, 2018

The need to analyze, synthesize and process three-dimensional objects is a fundamental ingredient in numerous computer vision and graphics tasks. In this talk, I will show how several geometric notions related to the Laplacian spectrum provide a set of tools for efficiently manipulating deformable shapes. I will also show how this framework combined with recent ideas in deep learning promises to bring shape processing problems to new levels of accuracy.
 October 10, 2017
October 10, 2017

The need to compute correspondence between three-dimensional objects is a fundamental ingredient in numerous computer vision and graphics tasks. In this talk, I will show how several geometric notions related to the Laplacian spectrum provide a set of tools for efficiently calculating correspondence
 July 21, 2017
July 21, 2017

A CVPR tutorial (together with Michael Bronstein and Maks Ovsjanikov) giving an overview of modern approaches to spectral 3D shape analysis.
 February 8, 2016
February 8, 2016

Three important properties of classification machinery are: (i) the system preserves the core information of the input data; (ii) the training examples convey information about unseen data; and (iii) the system is able to treat differently points from different classes. In this talk, I will show that these fundamental properties are satisfied by the architecture of deep neural networks. I will highlight a formal proof that such networks with random Gaussian weights perform a distance-preserving embedding of the data, with a special treatment for in-class and out-of-class data. Similar points at the input of the network are likely to have a similar output. The theoretical analysis of deep networks I will present exploits tools used in the compressed sensing and dictionary learning literature, thereby making a formal connection between these important topics. The derived results allow drawing conclusions about the metric learning properties of the network and their relation to its structure, as well as providing bounds on the required size of the training set such that the training examples would represent faithfully the unseen data. I will show how these conclusions are validated by state-of-the-art trained networks. I believe that these results provide an insight into why deep learning works and potentially allow designing more efficient network architectures and learning strategies.
 Novebmer 7, 2014
Novebmer 7, 2014

Graphs are a ubiquitous mathematical abstraction employed in numerous problems in science and engineering. Of particular importance is the need to find best structure-preserving matching of graphs. Since graph matching is a computationally intractable problem, numerous heuristics exist to approximate its solution. An important class of graph matching heuristics is relaxation techniques based on replacing the original problem with a continuous convex program. Conditions for applicability or inapplicability of such convex relaxations are poorly understood. In this talk, I will show easy to check spectral properties characterizing a wide family of graphs for which equivalence of convex relaxation to the exact graph matching is guaranteed to hold.